Aprendeu que quando os protões chocam a energias tão elevadas como as do LHC, a colisão dá origem a uma mar de partículas de topos os tipos, aquelas que constituem a matéria à nossa volta, e outras que terão existido por breves instantes apenas logo após o Big Bang, ou em outros fenómenos ultra-violentos (ou quando criadas em Laboratório). As novas partículas são, em geral, muito mais pesadas que as partículas que colidiram, devido à relação E=mc². Simplesmente, toda a energia posta numa colisão pode ser convertida em massa! Numa colisão protão-protão, "tudo" pode acontecer, se alguns princípios elementares forem respeitados, como a conservação da energia e do momento linear. O seu desafio aqui é seleccionar acontecimentos em que tenha sido produzido um bosão Z⁰, uma partícula muito pesada com uma vida média muitíssimo curta. Em média vive apenas 3x10^-25 segundos, isto é, 0,0000000000000000000000003 s! Não há instrumentos que possam detectar algo num tempo tão curto. Como é que se pode então reconhecer a produção de um bosão Z⁰? Resposta: pela forma como decai ou como "morre". A partir dos diagramas de Feynman explicados noutro capítulo, você familiarizou-se com os vários modos de decaimento do bosão Z⁰. Os produtos destes decaimentos são suficientemente estáveis para atravessarem partes do detector e deixarem informação para ser gravada. Que sorte, hem? Para se lembrar dos decaimentos do bosão Z⁰, volte à página dos decaimentos do bosão Z⁰.

O truque para "garantir" que foi de facto produzido um bosão Z⁰ na colisão, é não só reconhecer os seus produtos de decaimento, como por exemplo um par muão-anti-muão ou electrão-positrão, mas também reconstruir a massa do bosão Z⁰. Pode obtê-la usando a massa, energia, e momento linear dos produtos de decaimento do bosão Z⁰. Como é que isto funciona? Mais uma vez precisa da equação E=mc² e da seguinte lei da natureza: a energia e o momento linear são conservadas(os) em qualquer processo na natureza. Os seus valores antes e depois da colisão ou do decaimento são os mesmos.
Para ter sucesso nesta parte, precisará de saber o que é eV (electrão-Volt), momento (linear), e o que é um vector. Visite as páginas Ajuda 1: Unidades de Energia, Ajuda 2: Momento Linear ou Ajuda 3: Vectores, respectivamente, se quiser aprender sobre estes tópicos.

A física de partículas e altas energias usa uma unidade de energia diferente da unidade usada no dia-a-dia. É que as energias medidas são muito pequenas, e portanto a energia total também é muito pequena. Assim, em vez de usarmos o popular Joule, é mais conveniente usar o electrão-Volt. Com esta unidade, pode-se falar de 1 GeV (1 Giga electrão-Volt) em vez de 1,6x10^-10J (0.000000000016 Joule). Se quiser saber mais sobre como converter umas unidades noutras, visite a página Ajuda 1: Unidades de Energia.

No dia a dia, o momento linear é definido pelo produto da massa pela velocidade de um objecto: 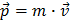. Contudo, no LHC quase todas as partículas, antes ou depois das colisões, têm quase a velocidade da luz no vazio (c=299 792 458 m/s). Por exemplo os protões colidem com velocidade v=0,999999991 c. Portanto é indispensável o uso da Teoria da Relatividade Restrita de Einstein, em que a fórmula para o momento linear é um pouco mais complicada mas ainda assim acessível:

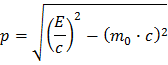
Se quiser saber como derivar esta fórmula, siga Ajuda 2: Momento.

Na fórmula
,
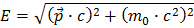E é a energia da partícula, p é o módulo do seu momento linear e m é a massa da partícula em repouso. Acontece que esta definição de massa é invariante na Natureza, isto é, é igual para todos os observadores. Mudando a fórmula obtemos:



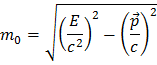
Como esta quantidade é invariante, e como a energia e momento linear são conservados, podemos reconstruir a massa do bosão Z⁰: mede-se as energias e momentos lineares dos produtos de decaimento, e as somas destes têm de ser as mesmas do bosão Z⁰, porque são quantidades conservadas. Imediato e simples, não parece? No caso de um bosão Z⁰ decair para um par electrão-positrão, a soma das suas energias e dos seus momentos lineares dá-nos a massa do bosão Z⁰ através da expressão:



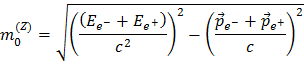
Com um pouco mais de manipulação matemática obtemos:



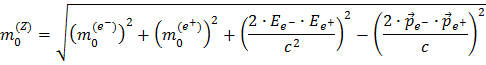
Você usou então o facto que E_Z = E_e^- + E_e⁺ e 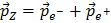, mais alguns truques. Se quiser compreender a demonstração completa veja aqui.
Afortunadamente o Detector ATLAS pode medir todas as quantidades desta fórmula de cima.

Como é que podemos partir de 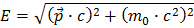para a fórmula simples que todos conhecemos: 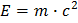? O que quer isto dizer fisicamente?

Pode usar um histograma para representar o seu conjunto de valores de massa para o bosão Z⁰. Um histograma é apenas uma forma de mostrar quantas vezes obtivemos um dado valor ao realizar uma certa medida. Por cada valor de massa calculado, você soma mais um ao resultado correspondente no histograma.

• Languages
• Página inicial
• Conteúdo
• Divulgação
• Contacto
• Descargas