Conteúdo
Massa Invariante
Como já aprendeu, a fórmula relativística para a energia de uma partícula é
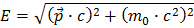
De forma a calcular a massa do bosão Z0, começamos com a fórmula para a massa dada pela soma das energias e dos momentos lineares dos produtos de decaimento:
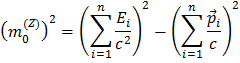
Como estamos a olhar para decaimentos do Z0 num par electrão-positrão ou num par muão-anti-muão, a soma é apenas para duas partículas, obtendo-se
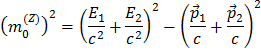
Retirando os parêntesis:
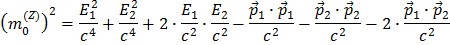
Pode reconhecer a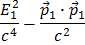 
como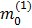 
, e o mesmo para a partícula 2 (mudando os termos da fómula (1)).
Assim pode concluir que
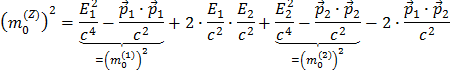
que, após alguma limpeza, nos dá
Tirando a raíz quadrada, obtém-se finalmente a expressão para a massa do Z0 em função das massas, energias e momentos das duas partículas resultantes do decaimento.
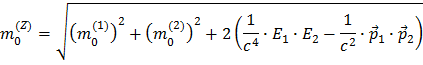
Assim precisa de conhecer todas estas quantidades para calcular a massa do Z0.
Aqui pode voltar para a página de medida do Z0.