Conteúdo
Ajuda 3: Vectores
Pode reparar que há uma seta sobre o momento linear:
.
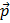Pode lembrar-se que a definição comum do momento linear é o produto da massa pela velocidade:
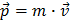e pode ver que a velocidade também tem uma seta. A seta quer dizer que a quantidade é um vector. E por vector entende-se algo que tem intensidade (ou tamanho), direcção e sentido. Isto é compreensível porque se tem uma velocidade com uma certa intensidade, está ao mesmo tempo dirigindo-se numa direcção para um determinado sentido. Ao realizar operações matemáticas com vectores, temos de os tratar com cuidado. É necessário decompor o vector em componentes segundo direcções x, y e z do nosso sistema de coordenadas. Assim, o produto interno entre dois momentos lineares define-se como:
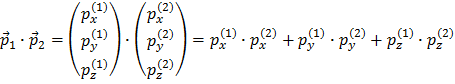
Não há componentes que misturem direcções diferentes. Repare também que não há setas sobre os termos resultantes. Isto é porque o produto interno ou produto escalar tem como resultado apenas um número (um escalar), o que quer dizer que não tem direcção.
Aqui pode voltar para a página principal da medida.