Vous venez d’apprendre que lorsque des protons entrent en collision avec des énergies aussi importantes que celle du LHC l’événement résultant produit une multitude de particules de tous types, des composants de la matière ordinaire comme des objets qui n’ont existé que peu de temps après le Big-bang. Ces nouvelles particules sont d’ordinaire bien plus massives que les protons qui sont entrés en collision grâce à la relation E=mc². Plus simplement : toute l’énergie injectée dans la collision peut réapparaître sous forme de masse ! Dans une collision proton-proton, « tout » peut se passer, pourvu que des principes importants soient respectés, par exemple la conservation de l’énergie. Votre défi consiste à sélectionner les événements dans lesquels un boson Z a été produit.
En fait ce sont les constituants des protons, quarks ou gluons, qui sont à l’origine de la création d’un boson Z, une particule lourde dont la durée de vie est très, très courte. Elle vit seulement 3 x 10^-25 seconds, soit 0.0000000000000000000000003 secondes ! Aucun instrument n’est capable de détecter un objet dans un laps de temps si court. Alors, comment peut-on « voir » le boson Z ? Réponse : par la connaissance de la manière dont il se désintègre ou « meurt ». En étudiant les diagrammes de Feynman dans un chapitre précédent vous vous êtes familiarisé avec les différents modes de désintégration du boson Z. Les produits de ces réactions sont suffisamment stables pour que le détecteur enregistre leur passage. Une chance non !? Pour rafraichir votre mémoire sur les désintégrations du Z, vous pouvez revenir à la page correspondante ici.

Pour acquérir la certitude qu’un boson Z a vraiment été créé lors de la collision, il ne suffit pas d’identifier ses produits de désintégration, comme des paires muon-antimuon ou électron-positron ; il faut également reconstruire la masse du boson Z. Pour cela, on utilise les masses, énergies et impulsions des particules émises par le Z. Comment faire ? A nouveau il faut utiliser l’équation E=mc² et quelques lois fondamentales vérifiées par la Nature comme les conservations de l’énergie et de l’impulsion. Les valeurs totales de ces quantités sont donc identiques avant et après la désintégration.
Pour mener à bien ces calculs vous devez savoir ce que sont un électron volt (noté « eV » en abrégé), une impulsion (ou quantité de mouvement) et un vecteur. Visiter l’un des liens Aide 1 : unités d’énergie, Aide 2 : impulsion ou Aide 3 : vecteurs pour en apprendre plus sur l’un ou l’autre de ces sujets.

Les physiciens des hautes énergies utilisent une unité d’énergie différente de celle dont on se sert dans la vie courante. Cela vient du fait que toutes les quantités mesurées sont extrêmement petites, en particulier l’énergie totale en jeu lors des collisions. Il est donc plus intéressant de remplacer le joule bien connu par l’électron volt. Ce choix permet de parler d’1 GeV (gigaélectron volt) au lieu de 1,6x10^-10J (0.000000000016 joule). Si vous souhaitez apprendre comment convertir des énergies d’une unité à l’autre, allez lire la page Aide 1 : unités d’énergie.

Dans la vie de tous les jours, l’impulsion (ou quantité de mouvement) d’un objet est définie comme le produit de sa masse par sa vitesse. 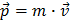. Mais, au LHC, toutes les particules présentes avant et après les collisions se déplacent presqu’à la vitesse de la lumière (v=0,999999991c). Il faut donc utiliser la théorie de la relativité restreinte d’Einstein, un cadre dans lequel la formule définissant la quantité de mouvement est un peu plus compliquée mais… toujours compréhensible.

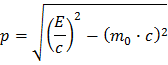
Si vous voulez comprendre comment obtenir cette formule, suivez le lien Aide 2 : impulsion.

Dans la formule
,
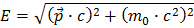E est l’énergie de la particule, p son impulsion et m sa masse au repos. Cette quantité est conservée dans la Nature. En manipulant cette équation on obtient :



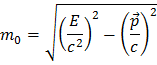
Puisque cette quantité est conservée, on peut s’en servir pour reconstruire la masse du boson Z. On mesure l’énergie et l’impulsion de chacun des produits de la désintégration et la « somme » de toutes ces quantités doit être égale à la masse du boson Z puisque rien ne se perd lors de ce processus. Tout cela est assez simple et direct n’est-ce-pas ? Dans le cas où un boson Z se désintègre en une paire électron-positron, la somme des énergies et des impulsions de l’électron et du positron conduit à la masse du boson Z de la manière suivante :



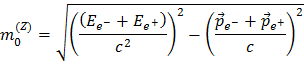
Après quelques manipulations mathématiques supplémentaires, on obtient :



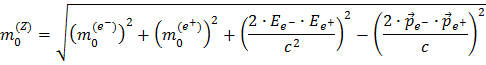
Ici nous avons utilisé les relations _Z = E_e^- + E_e⁺ et 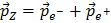, ainsi que d’autres astuces. Si le calcul complet vous intéresse, regardez ici. Heureusement le détecteur ATLAS peut mesurer toutes les quantités qui apparaissent dans la formule ci-dessus.

Mais comment passe-t-on de la formule 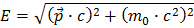à l’équation que tout le monde connaît : 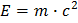? Que signifie-t-elle physiquement ?

Vous allez utiliser un histogramme pour résumer et afficher votre ensemble de masses mesurées pour le boson Z. Il s’agit d’une manière pour représenter combien de fois une valeur donnée d’une quantité mesurée (par exemple une masse) a été observée. Chaque fois que vous calculez une masse, entrez le résultat dans un histogramme.

• Languages
• Page d’accueil
• Plan du site
• A propos
• Contact
• Téléchargements