You have learned that when protons collide with such large energies as at the LHC, the collision results in a sea of all types of particles, the ones usual matter is made of, and others that only existed just after the Big Bang. The new particles are usually much heavier than the original colliding particles, thanks to the relation E=mc². To say it simply: All the energy we put into the collision can come out as mass instead! In a proton-proton collision “anything” can happen, provided some important principles are respected, such as energy conservation. Your challenge here is to select collisions where a Z boson was produced.

It is in fact the collision of the constituents of protons, quarks or gluons, which results in the creation of a Z boson, a heavy particle with a very, very short lifetime. It only lives for 3x10^-25 seconds, that is 0.0000000000000000000000003 seconds! No instruments are able to detect anything in that short a time. How can you “see” the Z boson then? Answer: By the knowledge of how it decays or "dies". From the Feynman diagrams in an earlier chapter, you got familiar with several ways the Z boson can decay. These decay-products are stable enough for the detector to register them. Lucky, huh? To refresh your memory on the Z decays, you can go back to Z boson decays here.

The trick you will use to be pretty sure that an actual Z boson was created in the collision, is not only to recognize the decay products, such as muon-antimuon or electron-positron pairs, but also to reconstruct the Z boson mass. You can do this by using the mass, energy and momentum of the Z boson's decay products. How does this work? Again you need to use E=mc², and a couple of fundamental laws of nature: Energy and momentum are conserved in any process in nature. Their values before and after the collision or decay are the same.

To succeed in this part, you need to know what eV (electron Volt) is, what momentum is, and what a vector is. Go to Help 1: Energy units, Help 2: Momentum or Help 3: Vectors to learn about these topics.

High-energy particle physics uses a unit of energy which is somewhat different from that of everyday life. This is because what is measured is extremely small, so is the total energy involved als very very small. Therefore, instead of using the well-known quantity Joule, it is more convenient to replace it by the electron-Volt. With this unit you can say 1 GeV (Giga electron Volt) instead of 1,6x10^-10J (0.000000000016 Joule). If you want to understand how to convert your numbers from one unit to another, follow Help 1: Energy units.

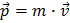In everyday life, momentum is defined as the mass times the velocity of some object: . However, at the LHC all the particles both before and after the collisions travel almost at the speed of light (v=0,999999991c). You therefore have to use the theory of special relativity of Einstein, and the formula for momentum is a bit more complicated but still manageable:



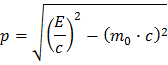
If you want to find out how to derive this formula, follow Help 2: Momentum.

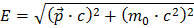In the formula , E is the energy of the particle, p is the momentum and m₀ is the mass of the particle when at rest. It so happens that this definition of mass is conserved in Nature. Shuffling the formula we get:



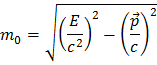
Since this quantity is conserved we can use it to reconstruct the Z boson mass: You measure the energy and momenta of the decay products, and the "sum" of these have to be the same as the mass of the Z boson, since what comes in must go out. Quite straightforward and simple, isn't it? In the case of a Z boson decaying to an electron-positron pair the sum of energies and momenta of the electron and positron lead to the mass of the Z boson in the following way:



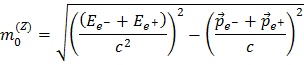
With a bit more mathematical juggling we get:



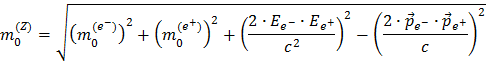
Then you have used that E_Z = E_e^- + E_e⁺ and 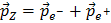, plus some other tricks. If you want to understand the full derivation look here.

Luckily, the ATLAS detector can measure all the quantities in this formula above.

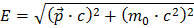How can we arrive from to the simple formula everyone knows: 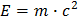? What does this mean physically?

You will make use of a histogram to plot or summarize your set of masses of the Z boson. A histogram is just a way of displaying how many times a certain value of a certain measured variable occured. For each mass you calculate, you enter the result into the histogram.

• Languages
• Homepage
• Content
• Imprint
• Contact
• Downloads