Momento (Linear)
No dia a dia, o momento (linear, ou quantidade de movimento) de um objecto é definido pelo produto da sua massa pela sua velocidade: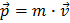 
. Contudo, no LHC, todas as partículas antes e depois das colisões viajam quase à velocidade da luz no vazio, c (v=0,999999991c para os protões acelerados). É necessário utilizar a Teoria da Relatividade Restrita de Einstein, em que a fórmula para o momento é um pouco mais complicada, mas ainda compreensível.
Começamos pela famosa fórmula de Einstein
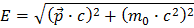
Aqui E significa energia, p significa o módulo do momento, m significa massa (em repouso), e c significa a velocidade da luz no vazio. Momento é um vector, e se tiver dificuldades sobre vectores, siga para Vectores.
Depois de um bocadinho de álgebra, pode-se exprimir o módulo do momento como uma função da energia e da massa:
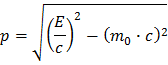
Em todos os processos na Natureza o momento é conservado. Isto significa: o que entra tem que sair, o que nas nossas colisões de partículas quer dizer (lembrando que o momento é um vector) pantes=pdepois. Para um Bosão Z decaindo num para electrão-positrão isto traduz-se na equação pZ = pe- + pe+.
Pergunta: na versão do dia-a-dia para o momento p=mv, temos um problema para partículas sem massa como o fotão: o seu momento seria 0. O que se passa com o momento no caso de uma partícula sem massa na versão do momento na Teoria da Relatividade Restrita?