Bsp Feyn-graph theo-3

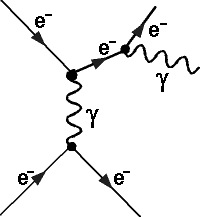
Beispiele von Feynman-Diagrammen des Elektromagnetismus:
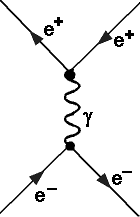
Elektron-Positron Streuung Lässt man Elektronen auf Positronen stoßen, so kann man manchmal nach dem Stoß wieder ein Elektron und ein Positron beobachten, die sich aber in eine andere Richtung bewegen.Will man diesen Streuprozess e⁺e^- -> e⁺e^- in Feynman Diagrammen beschreiben, so geht das in der elektromagnetischen Wechselwirkung am einfachsten über ein virtuelles Photon, wobei die zwei unten abgebildeten Diagramme möglich sind. Beide Prozesse (und alle anderen hier nicht abgebildeten komplizierteren Möglichkeiten) müssen bei der Berechnung addiert werden. Da das virtuelle Photon nicht beobachtbar ist, kann man prinzipiell durch eine Messung nicht unterscheiden, welcher Prozess stattgefunden hat.
Streuung	Vernichtung
Hier sind die Grundprozesse der Abstrahlung und des Einfangs eines virtuellen Photons kombiniert. Es spielt dabei keine Rolle, ob das Elektron oder das Positron das Photon abstrahlt (einfängt).	Hier sind die Grundprozesse der Paarvernichtung in ein virtuelles Photon und die anschliessende Paarerzeugung durch dieses Photon kombiniert.
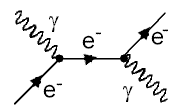
Compton Streuung Der Streuprozess von Photonen an Elektronen e^- -> e^- ist als Compton Streuung bekannt. Man behandelt ihn meist als elastischen Stoß, bei dem das Photon einen Teil seiner Energie abgibt. Wie man an den abgebildeten Feynman Diagrammen sieht, ist dieses Bild des elastischen Stoßes nicht ganz richtig: das einlaufende Photon wird nämlich immer völlig absorbiert, und es entsteht (davor oder danach) ein neues auslaufendes Photon. Trotzdem stimmen die Rechnungen des elastischen Stoßes, weil sie nur den Impuls- und Energieerhaltungssatz verwenden, der eben auch für die beiden folgenden Diagramme gilt.

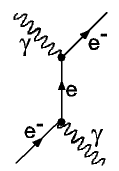
Hier ist wieder der Grundprozess des Einfangs eines Photons kombiniert mit.der Abstrahlung eines anderen Photons. Im Unterschied zur e⁺e^- Streuung von oben, sind aber die Photonen als ein-und auslaufende Teilchen messbar (haben Masse Null). Das Elektron wird dagegen nach dem Einfang des Photons erst einmal virtuell (mit einer Masse von mehr als 0,5 MeV), und bekommt erst am Schluß wieder seine normale Masse.	Auch in diesem Diagramm haben wir es mit meßbaren Photonen und einem virtuellen e zu tun, das allerdings hier senkrecht gezeichnet ist, und daher nicht eindeutig als Elektron oder Positron identifizierbar ist. Dies ist eine abkürzende Darstellung für die beiden unten stehenden Prozesse, die man erhält, wenn man dieses Diagramm etwas "verbiegt". Je nach Richtung der Verbiegung erhält man dann mit Hilfe der Regeln für die Pfeilrichtung in Feynman Diagrammen entweder ein Elektron oder ein Positron.
Im linken Bild entsteht der Compton Prozess aus einer Abfolge von Abstrahlung und Einfang eines messbaren Photons durch ein Elektron, in genau umgekehrter Reihenfolge zu oben. Vor dem Photon-Einfang ist das Elektron wieder virtuell. Im rechten Bild erfolgt erst eine Paarerzeugung von Elektron und virtuellem Positron durch das einfallende Photon. Das virtuelle Positron verschwindet durch Paarvernichtung mit dem einfallenden Elektron.
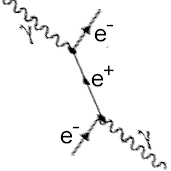
Elektron-Bremsstrahlung Ein anfliegendes Elektron tauscht mit einem Elektron einer Atomhülle ein virtuelles Photon aus und strahlt danach ein meßbares Photon ab. Die Abstrahlung dieses Photons nennt man Bremsstrahlung und kann - wie hier- im elektrischen Feld eines Elektrons aber auch im elektrischen Feld von anderen Teilchen, insbesondere von Atomkernen, passieren. In der Teilchenphysik versteht man also den Einfluss eines elektrischen Feldes auch als Austausch von virtuellen Photonen.
Dies ist ein Beispiel für einen Prozess, dessen Feynman-Diagramm eine ungerade Anzahl von Vertices besitzt. Es treten zwei virtuelle Teilchen auf: das ausgetauschte Photon, und das "obere" Elektron vor der Bremsstrahlung. Es existiert auch ein (hier nicht abgebildetes) zweites Diagramm, bei dem das Bremsstrahlungsphoton vom einlaufenden, und nicht vom auslaufenden Elektron abgestrahlt wird.
Alles verstanden? Hier ein kleines Quiz zur Compton Streuung
	Weiter beide Level