Innhold
Invariant masse
Som du allerede har lært er formelen for relativistisk energi av en partikkel
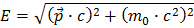
For å kalkulere massen av Z bosonet starter vi med formelen for Z massen som en sum av energier og massefart av henfallsproduktene:
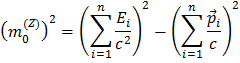
Siden vi ser på Z henfall til enten et elektron-positron par eller et myon-antimyon par blir det en sum over bare to partkler, som gir
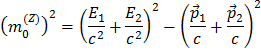
Multiplisere ut parentesene:
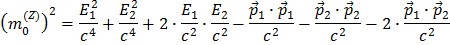
Du gjenkjenner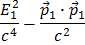 
som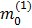 
og likeledes for partikkel 2, (fra ombytting av termene i formel (1)).
Så du ser at
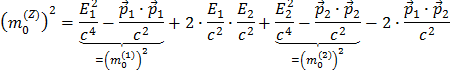
som, etter rydding, gir
Ved å ta kvadratroten får du det endelige uttrykket for Z massen uttrykt ved masser, energier og massefart av de to henfallspartiklene.
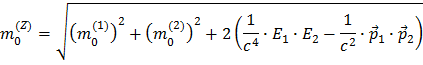
Du trenger derfor å kjenne til alle disse verdiene for å kunne beregne Z massen.
Her kommer du tilbake til Z målesiden