Medida- Conceptos, definiciones y métodos
El nacimiento, vida y muerte del bosón Z
Has aprendido que cuando los protones colisionan con tanta energía como en el LHC los resultados de la colisión sonun mar de todo tipo de partículas, las que forman la materia ordinaria y las que solo existían justamente tras el Big Bang. Las nuevas partículas son, usualmente, mucho más pesadas que las partículas colisionantes, gracias a la relación E=mc2. Para decirlo simplemente. ¡Toda la energía puesta en la colisión se transforma en masa!. En una colisión protón-protón puede ocurrir "cualquier caso", supuesto que se respeten algunos principios importantes, tales como la conservación de energía. Tu reto aquí es seleccionar las acolisiones en las que se ha producido un bosón Z
De hecho es la colisión de los constituyentes de los protones, quarks o gluones, lo que produce la creación de un bosón Z, una partícula pesada, con una vida media muy, muy corta. Solo vive durante 3 x 10-25 segundos, es decir ¡0.0000000000000000000000003 segundos!. Ningún instrumento es capaz de detectar nada en tan pequeño espacio de tiempo. ¿Cómo puedes "ver", entonces, el bosón Z? Respuesta: Por el conocimiento de como decae o "muere". De los diagramas de Feynman en un capítulo anterior, estás familiarizado con diversas formas de desintegración del bosón Z. Estos productos de desintegración son suficientemente estables para que el detector los registre. ¿Qué suerte, eh?. Para refrescar tu memoria sobre las desintegraciones del Z, puedes vover a las desintegraciones del Z aquí.

Recosntruyendo la masa del bosón Z
El truco que utilizarás para estar bien seguro de que un bosón Z fue creado en la colisión, nosolo es reconocer los productos de desintegración, como pares electrón-positrón o muon-antimuon, sino reconstruir también la masa del bosón Z. Puedes hacerlo usando la masa, energía y momento de los productos de desintegración del bosón Z. ¿Cómo funciona?. De nuevo necesitas usar E=mc2, y una pareja de leyes fundamentales de la Naturaleza: la conservación de la energía y el momento en cualquier proceso natural. Sus valores deben ser iguales antes y después de la colisión.
Para triunfar en este apartado necesitas saber que es eV( electrón-voltio), que es momento, y que es un vector. Vete a Ayuda 1: Unidades de energía , Ayuda 2: Momento o Ayuda 3: Vectores para aprender acerca de estos tópicos

Unidad de energía en física de partículas
La física de partículas usa una unidad de energía que es algo diferente de la de uso habitual. Esto es debido a que lo que se mide es extremadamente pequeño, de modo que la energía total a considerar es muy,muy pequeña. Por ello, en lugar de usar una cantidad bien conocida, el julio, es mejopr reemplazarla por el electrón-voltio. Con esta unidad puedes decir 1 GeV (Giga electrón-voltio) en lugar de 1,6x10-10J (0.000000000016 julios). Si quieres entender como convertir tus números de una a otra unidad, sigue Ayuda 1: Unidades de energía.

Momento
En el uso habitual, el momento se define como el producto de la masa por la velocidad de algún objeto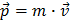momentum definition. Sin embargo, en LHC todas las partículas viajan a la velocidad de la luz( v=0,999999991c), antes y después de la colisión. Por ello tienes que utilizar la teoría de la relatividad especial de Einstein y la fórmula para el momento es un poco más complicada, aunque todavía manejable

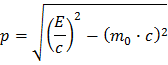
momentum definition in special relativity


Si quieres encontrar cómo derivar esta fórmula, sigue Ayuda 2: Momento.



Masa en reposo
En la fórmula
simple relativistic relationsip between energy, momentum and mass,

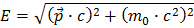E es la energía de la partícula, p es el momento y m es la masa de la partícula cuando está en reposo. Ocurre que esta definición de masa se conserva en la Naturaleza. Barajando la fórmula obtenemos:

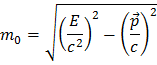
simple relativistic relationsip between energy, momentum and mass


Como esta cantidad es conservada podemos usarla para reconstruir la masa del bosón Z:mides la energía y momento de los productos de desintegración, y la "suma" de éstos debe ser la misma que la masa del bosón Z, ya que lo que se crea es igual que lo que se destruye. Demasiado directo y sencillo ¿no?. En el caso de un bosón Z decayendo en un par electrón-positrón la suma de las energías y momentos del electrón y positrón conducen a la masa del bosón Z en la forma siguiente:

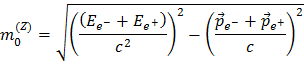
simple relativistic relationsip between energy, momentum and mass


Con un poco más de malabarismo matemático obtenemos:

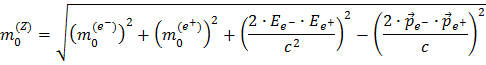
simple relativistic relationsip between energy, momentum and mass


Entonces has usado que EZ = Ee- + Ee+ y 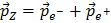, más algunos otros trucos. Si quieres entender la derivación completa mira aquí.
Afortunadamente, el detector ATLAS puede medir todas las cantidades de las fórmulas de arriba

Cuestión de prueba
¿Cómo podemos llegar de 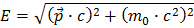simples parentescos relativistas entre energía, momento y masa a la sencilla fórmula de todos conocida: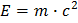imples parentescos relativistas entre energía, momento y masa? ¿Qué significa físicamente?

Histograma
Utilizarás un histograma para dibujar o sumarizar tu conjunto de masas del bosón Z. Un histograma es justamente un modo de mostrar cuantas veces ocurre un valor concreto de cierta variable medida. Por cada masa calculada, pones el resultado en el histograma.