Contenido
Masa Invariante
Como ya has aprendido, la fórmula para la energía relativista de una partícula es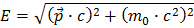
Para calcular la masa del bosón Z partiremos de la fórmula para la masa del Z como una suma de energías y momentos de las partículas de desintegración:
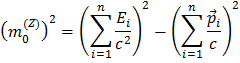
Como estamos mirando desintegraciones del Z, ya sea en un par electrón-positrón o un par muon-antimuon, la suma se realiza sobre dos partículas solamente, dando
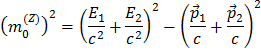
Multiplicando los paréntesis
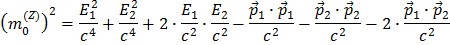
Puedes reconocer la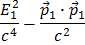 
como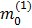 
y equivalentemente para la partícula 2, (de jugar con los términos de la fórmula (1))
Así ves que
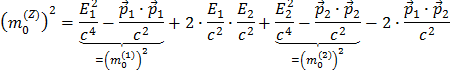
lo cual, una vez limpiado, da
Tomando la raíz cuadrada te da la expresión final de la masa del Z expresada en términos de las masas, energías y momentos de las dos partículas de la desintegración
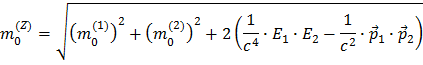
Por tanto necesitas conocer todas esas cantidades para calcular la masa del Z
Aquí vuelves al lugar de las medidas de Z