Du har lært, at når protoner støder sammen ved så høje energier som i LHC, så resulterer kollisionerne i alle mulige slags partikler, både dem normalt stof består af og andre, som kun eksisterede lige efter Big Bang. De nye partikler er normalt meget tungere end de partikler som oprindeligt stødte sammen, takket være relationen E=mc². Forenklet sagt: Al den energi vi putter ind i en kollision kan komme ud som masse i stedet for! I en proton-proton kollision kan "hvad som helst" ske, under forudsætning af at nogle vigtige regler overholdes, som f.eks. bevarelse af energi. Udfordringen til dig er at udvælge kollisioner, hvor der blev produceret en Z boson.
Det er i virkeligheden sammenstødet mellem bestanddele af protonen, kvarker eller gluoner, som resulterer i skabelsen af en Z boson, som er en tung partikel med en meget, meget kort levetid. Den lever kun i 3 x 10^-25 sekunder, dvs. 0.0000000000000000000000003 sekunder! Der findes ingen instrumenter der kan detektere noget på så kort tid. Hvordan kan man så "se" Z bosonen? Svar: Ved at bruge sin viden om hvordan den henfalder eller "dør". Fra Feynman diagrammerne i et tidligere afsnit kender du flere af de måder en Z boson kan henfalde på. Henfaldsprodukterne er tilstrækkeligt stabile til at detektoren kan registrere dem. Heldigt, hvad? For at genopfriske din viden om Z henfaldene kan du gå tilbage til Z boson henfald her.

Det trick du skal bruge for at være ret sikker på at der virkelig blev skabt en Z boson i kollisionen er ikke blot at genkende dens henfaldsprodukter, som f.eks. et myon-antimyon eller et elektron-positron par, men også at rekonstruere Z bosonens masse. Det kan man gøre ved at benytte massen, energien og impulsen af Z bosonens henfaldsprodukter. Hvordan virker det? Igen skal du bruge E=mc² og et par fundamentale naturlove: energi og impuls er bevarede i enhver proces i naturen. De samlede værdier før og efter kollisionen eller henfaldet er derfor de samme.
For at klare denne del skal du vide hvad eV (elektronvolt) er, hvad impuls er og hvad en vektor er. Gå til Hjælp 1: Energienheder, Hjælp 2: Impuls eller Hjælp 3: Vektorer

Højenergi partikelfysik bruger en energienhed, som er noget forskellig fra den vi bruger i hverdagen. Det er fordi det vi måler er meget småt, så den totale energi også er meget meget lille. Derfor er det nemmere, i stedet for at bruge den velkendte størrelse Joule, at erstatte den med enheden elektronvolt. Med denne enhed kan man sige 1 GeV (Giga elektronvolt) i stedet for 1,6x10^-10J (0.000000000016 Joule). Hvis du vil vide hvordan man omregner fra den ene enhed til den anden, så følg Hjælp 1: Energi enheder.

I hverdagen er impuls defineret som massen gange med hastigheden af et eller andet objekt.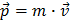. I LHC bevæger alle partiklerne sig imidlertid både før og efter kollisionerne med næsten lysets fart (v=0,999999991c).Derfor er man nødt til at bruge Einsteins specielle relativitetsteori, hvor formlen for impuls er en smule mere kompliceret, men stadig til at benytte: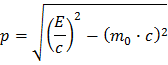

Hvis du vil vide hvordan man kan udlede denne formel, så følg Hjælp 2: Impuls.

I formlen
,
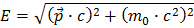er E energien af partiklen, p er dens impuls og m er dens masse når den er i hvile. Det viser sig at denne definition af masse er bevaret i naturen. Ved at omordne formlen får vi:



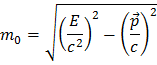
Da denne størrelse er bevaret kan vi bruge den til at rekonstruere Z bosonens masse: Man kan måle energien og impulsen af dens henfaldsprodukter, og ud fra summen af dem beregne massen af Z bosonen, fordi hvad der kommer ind må kommer ud igen. Helt ligetil og enkelt, ikke? I tilfældet hvor Z bosonen henfalder til et elektron-positron par, fører summen af energier og impulser af elektronen og positronen til massen af Z bosonen sådan:



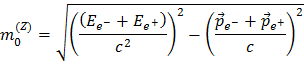
Ved lidt flere matematiske omskrivninger får vi:



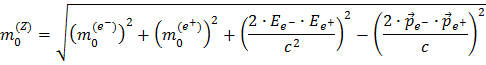
Så skal man bruge at E_Z = E_e^- + E_e⁺ and 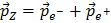, plus nogle andre tricks. Hvis du vil vide hvordan hele udledningen ser ud, så se her.
Heldigvis kan ATLAS detektoren måle alle størrelserne i formlen ovenfor.

Hvordan kan man komme fra 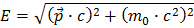til den simple formel som alle kender: 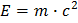? Hvad betyder det fysisk?

Du kommer til at bruge et histogram for at plotte eller opsummere dine målinger af massen af Z bosonen. Et histogram er blot en måde at vise, hvor mange gange en bestemt værdi af en eller anden målt størrelse er forekommet: For hver masse du beregner sætter du svaret ind i histogrammet.

• Languages
• Hjemmeside
• Indhold
• Webmaster
• Kontakt
• Downloads