Du hast gelernt, dass das Ergebnis der hochenergetischen Kollisionen von Protonen am LHC ein See aus allen Arten von Teilchen ist, sowohl solche der gewöhnlichen Materie als auch solche wie sie direkt nach dem Urknall existierten. Die hervorgebrachten Teilchen sind wegen der Beziehung E=mc² für gewöhlich viel schwerer als die ursprünglich kollidierten Teilchen. Um es mit einfachen Worten zu sagen: Die insgesamt in die Teilchenkollision gesteckte Energie kann nach der Kollision in Masse vorliegen. In Proton-Proton-Kollisionen kann "alles" passieren, solange einige wichtige Prinzipien wie beispielsweise die Energieerhaltung erfüllt werden. Deine Herausforderung besteht darin, Ereignisse herauszufinden, in denen ein Z-Boson erzeugt wurde.

Genaugenommen kollidieren die Bestandteile des Protons - diese sind Quarks und Gluonen - miteinander und erzeugen ein Z-Boson, das ein sehr schweres Teilchen mit einer kurzen Lebensdauer ist. Es lebt gerade einmal 3 x 10^-25 Sekunden, also 0.0000000000000000000000003 Sekunden. Kein Geräte auf diesem Planeten sind in der Lage auch nur irgendetwas in solch einer kurzen Zeit nachzuweisen. Wie kannst Du dann das Z-Boson "sehen"? Die Antwort: Durch das Wissen wie es zerfällt oder dramatischer gesagt, wie es stirbt. Aus den Feynman-Diagrammen eines vorhergehenden Kapitels bist Du mit den verschiedenen Zerfallsmöglichkeiten des Z-Boson vertraut. Diese Zerfallsprodukte sind so stabil, dass sie mit dem Detektor nachgewiesen werden können. Ein Glück, was? Um Deine Erinnerung an den Zerfall des Z-Bosons aufzufrischen, kannst Du hier zur Webseite springen, auf der Du etwas über den Z-Zerfall erfährst.

Um wirklich sicher zu gehen, dass tatsächlich ein Z-Boson erzeugt wurde, wirst Du nicht einfach nur die Zerfallsprodukte (wie Myon und Antimyon oder Elektron und Positron) des Z-Bosons erkennen. Dein Kunstgriff wird vielmehr darin bestehen die Masse des Z-Bosons zu rekonstruieren. Du kannst dies mit Hilfe der Masse, der Energie und des Impulses der Zerfallsprodukte des Z-Bosons bewerkstelligen. Wie soll das funktionieren? Wiederum benötigst Du neben der Gleichung E=mc² ein paar grundlegende Naturgesetze: Energie und Impuls bleiben in allen Prozessen der Natur erhalten. Ihre Werte vor und nach einer Kollision oder eines Zerfalls gleich.

Um in diesem Teil der Masterclass erfolgreich sein zu können, musst Du wissen was eV (Elektronenvolt) und was Impuls ist und was Vektoren sind. Nutze die folgenden Links, um etwas über diese Themen zu lernen: Hilfe 1: Maßeinhaeit der Energie, Hilfe 2: Impuls or Hilfe 3: Vektoren.

In der Hochenergiephysik wird eine andere Maßeinheit für die Energie verwendet als im täglichen Leben. Dies liegt an der Größenordnung: Was dort gemessen wird is so klein, dass es zweckmäßiger ist, die bekannten Einheit Joule, mit der Einheit Elektronenvolt zu ersetzen. Bei dieser Einheit sagt man: 1 GeV (Gigaelektronenvolt) anstelle von 1,6x10^-10J (0.000000000016 Joule). Wenn Du wissen möchtest, wie Deine Maßzahlen von einer in die andere Einheit umgewandelt wird, folge der Hilfe 1: Maßeinheit der Energie.

Im täglichen Leben wird Impuls als Masse mal Geschwindigkeit eines Objektes definiert: 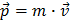. Wie dem auch sei, am LHC bewegen sich alle Teilchen sowohl vor als auch nach der Kollision mit angenähert Lichtgeschwindigkeit (v=0,999999991c). Daher musst Du Gebrauch von Einsteins spezieller Relativitätstheorie machen, wodurch sich die Gleichung für den Impuls ein wenig komplizierter, wenn auch immer noch handhabbar, gestaltet:



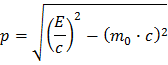
Wenn Du verstehen möchtest, wie diese Gleichung abgeleitet wird, folge der Hilfe 2: Impuls.

In der Gleichung
,
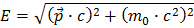ist E die Gesamtenergie, p der Impuls and m die Ruhemasse, des Teilchens. Diese Definition von Masse bleibt in der Natur ebenfalls erhalten. Stellen wir die Formel nach der Masse um, so erhalten wir:



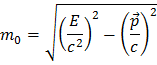
Da diese Größe erhalten bleibt, können wir sie benutzen, um die Masse des Z-Boson zu rekonstruieren: Du misst die Energie und den Impuls der Zerfalssprodukte und ihre "Summe" muss die Gleiche sein wie die des Z-Bosons, denn es gilt: was reingeht, muss auch wieder herauskommen. Geradezu einfach, oder nicht? Im Fall des Zerfalls des Z-Bosons in ein Elektron-Positron-Paar führt die Summe der Energien und des Impulses von Elektron und Positron sowie das Kennen ihrer Ruhemasse zur Masse des Z-Bosons:



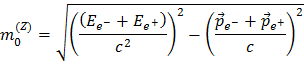
Nach ein paar mathematischen Kniffen erhalten wir:



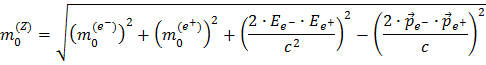
Dabei haben wir sowohl die Beziehungen E_Z = E_e^- + E_e⁺ und 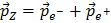als auch noch ein paar Tricks benutzt. Wenn Du die vollständige Ableitung der Gleichung verstehen willst, schau doch hier nach.

Glücklicherweise kann der ATLAS-Detektor alle Größen der oben zu findenden Gleichung messen.

Wie leitet man ausgehend von der Gle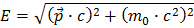ichung , die jedem bekannte Gleichung 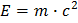her? Was bedeutet dies physikalisch?

Du wirst von Histogrammen Gebrauch machen, um Deinen Satz von Massen aus Z-Boson-Erfeignissen darzustellen. Ein Histogramm ist einfach eine eine Darstellung, wie viel mal ein bestimmter Wert (hier: Deine gemessenen Werte) einer bestimmten zu messenden Größ (hier: Masse des Z-Bosons) auftritt. Für jede berechnete Masse trägst Du Dein Ergebnis in das Histogramm ein.

• Sprachauswahl
• Startseite
• Inhalt
• Impressum
• Kontakt
• Downloads