Massa Invariante
Come hai appena imparato, la formula per l'energia relativistica di una particella è
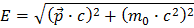(1)
Per calcolare la massa del bosone Z, inseriamo nella formula della massa la somma delle energie e delle quantità di moto delle particelle di decadimento:
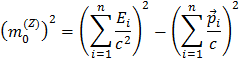
Dato che stiamo considerando decadimenti dello Z in una coppia elettrone-positrone o muone-antimuone, la somma è su sole due particelle, e fornisce quindi
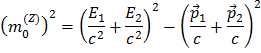
Risolvendo le parentesi:
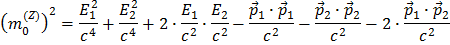
Puoi riconoscer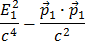e 
come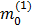 
e così pure la particella 2 (manipolando i termini nella formula (1)).
Così si vede che:
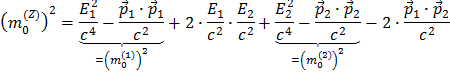
Che, dopo aver ripulito, ci dà:
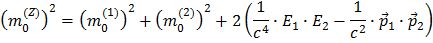
Facendo la radice quadrata si ottiene l'espressione finale della massa dello Z, in funzione delle masse, energie e quantità di moto delle due particelle di decadimento:
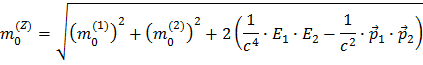
Quindi devi conoscere tutte queste quantità, per calcolare la massa dello Z.