Impulsion (ou quantité de mouvement)
Dans la vie de tous les jours, l’impulsion (ou quantité de mouvement) d’un objet est définie comme le produit de sa masse par sa vitesse: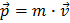 
. Mais, au LHC, toutes les particules présentes avant et après les collisions se déplacent presqu’à la vitesse de la lumière (v=0,999999991c pour un proton). Il faut donc utiliser la théorie de la relativité restreinte d’Einstein, un cadre dans lequel la formule définissant la quantité de mouvement est un peu plus compliquée mais… toujours compréhensible.
Nous commençons par la fameuse formule d’Einstein
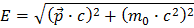
Ici le symbole E designe l’énergie, p l’impulsion, m la masse de la particule et c la vitesse de la lumière. L’impulsion (ou quantité de mouvement) est un vecteur, qui possède donc 3 projections selon les axes x, y et z; si le terme de vecteur ne vous dit rien, suivez le lien vecteurs.
En manipulant un peu cette équation, vous pouvez exprimer le module du vecteur impulsion en fonction de l’énergie et de la masse.
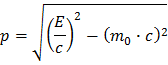
Dans la Nature l’impulsion totale est conservée. Cela signifie que ce qui arrive doit repartir ensuite ce qui, dans le cas de nos collisions entre particules, se traduit par la relation pavant=paprès. Pour un boson Z se désintégrant en une paire électron-positron, on obtient pZ = pe- + pe+.
Une question pour aller plus loin : si on applique la définition habituelle de l’impulsion p=mv on se heurte à un problème avec des objets sans masse comme le photon puisque cette relation donne une impulsion nulle. Que vaut l’impulsion d’une particule de masse nulle si on utilise l’équation valable en relativité restreinte ?