Identifier une particule en mesurant sa masse!
Attention! Vous êtes sur le point de vous familiariser avec un des concepts les plus importants en physique.
Dans la version complète de la formule d’Einstein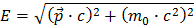 
, E est l’énergie de la particule, p sa quantité de mouvement (ou impulsion) et m0 sa masse au repos. Cette quantité se conserve et s’appelle « Masse Invariante ». En réarrangeant cette formule, on obtient :
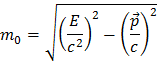
Puisque cette quantité est conservée, nous pouvons l’utiliser pour estimer la masse d’une particule (« mère ») qui s’est désintégrée. On mesure la somme des énergies et des impulsions (quantités de mouvement) de chacun des produits de désintégration de cette particule « mère » et on en déduit à partir de la formule ci-dessus sa masse – puisque rien ne se perd lors de ce processus. Tout ceci est assez simple et direct n’est-ce pas !?
Dans le cas où un Z0 se désintègre en une paire électron (e-) - positron (e+) la somme des énergies et des impulsions des électrons et des positrons conduit à la masse du Z0 de la manière suivante :
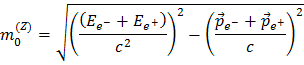
L’énergie EZ=Ee- + Ee+ et la quantité de mouvement (l’impulsion)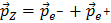 
du boson Z sont connues puisque le détecteur ATLAS peut mesurer l’énergie et l’impulsion de ses produits de désintégration. Cela signifie que vous avez tout ce dont vous aurez besoin pour calculer la masse du boson Z, ou celles d’autres particules comme le J/ψ ou l’Upsilon Υ.
En fait, cette méthode dite de la masse invariante fonctionne pour une grande variété d’états finaux – γγ, l+l- (l=e,μ), l+l-l+l-, etc. –, comme vous le constaterez vous-même en étudiant le boson Z, en cherchant le boson de Higgs et même en explorant l’Inconnu !