Les vecteurs
Vous avez sans doute remarqué qu’il y a une flèche au-dessus du symbole de l’impulsion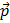 
. Vous vous souvenez qu’en physique classique, l’impulsion est égale au produit de la masse par la vitesse : 
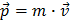et vous pouvez voir que la vitesse est également affublée d’une flèche. Cela signifie que cette quantité est un vecteur. Un vecteur se définit par sa taille, sa direction et son sens. C’est naturel car pour caractériser une vitesse il faut connaître sa valeur et la direction dans laquelle l’objet qui la porte se déplace. Les opérations mathématiques sur des vecteurs obéissent donc à des règles particulières. Un vecteur qui pointe dans une direction quelconque peut toujours être décomposé comme la somme de trois composantes, alignées dans les directions x, y et z du système de coordonnées. Ainsi, la multiplication entre deux impulsions donnera :
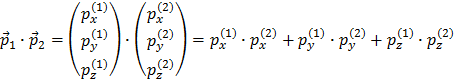
Aucun terme de cette formule ne mélange deux directions différentes : on multiplie les coordonnées selon l’axe x, puis celles selon l’axe y et enfin celles selon l’axe z et enfin on somme ces trois produits. Le résultat est un nombre (dans le jargon scientifique un « scalaire ») sans direction (et donc sans « flèche ») qui exprime le produit (scalaire) entre deux vecteurs.