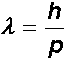Die
de-Broglie-Wellenlänge von Teilchen
|
Am Anfang des Jahrhunderts hat der Physiker De
Broglie herausgefunden, dass nicht nur elektromagnetische Wellen, sondern
auch Teilchenstrahlen eine 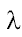Wellenlänge 
haben. Er hat den allgemeinen Zusammenhang zwischen dem Impuls p
eines beliebigen Teilchens und der damit verbundenen Wellenlänge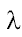
formuliert: |
|
|
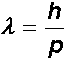
Mit der De-Broglie-Beziehung wird jedem Teilchen, das einen Impuls besitzt,
eine Wellenlänge zugeordnet. Damit wird eine Brücke zwischen der Welleneigenschaft
und der Teilcheneigenschaft geschlagen. Sinn macht die De-Broglie-Wellenlänge
allerdings nur für Teilchen des Mikrokosmos, wie z.B. Elektronen. D.h. man
kann hochenergetische Teilchen, deren Wellenlänge nach obiger Beziehung
sehr klein ist, zur Untersuchung verwenden. |
| Bei Stoßexperimenten mit hoher Energie erreicht
man einerseits sehr kleine De-Broglie-Wellenlängen und damit ein sehr hohes
Auflösungsvermögen , andererseits können damit sehr schwere Stoßprodukte
wie z.B. neue, bisher unbekannte Teilchen, erzeugt werden. Sehr schnelle
Elektronen der Gesamtenergie 1 GeV haben etwa eine Wellenlänge von 0.2 fm.
Mit Strahlen dieser Wellenlänge können folglich Strukturen im Bereich von
10-16 m aufgelöst werden. Ein Proton hat z. B. einen Durchmesser
von ca. 10-15 m, so dass mit solch hochenergetischen Elektronen
die inneren Strukturen des Protons untersucht werden können. |
|
Die Auflösung ergibt sich aus der De-Broglie-Wellenlänge
der Teilchen zu
|
|
|
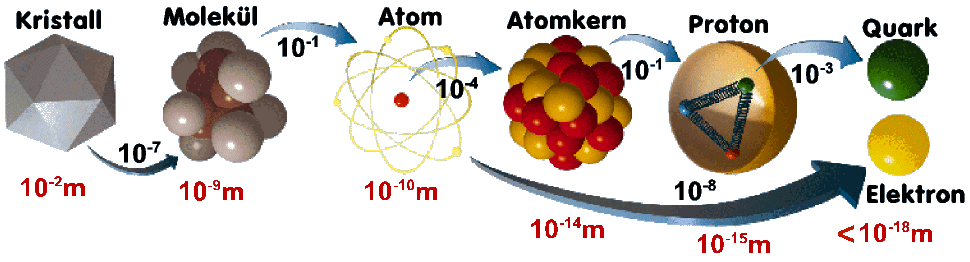
| Will man subatomare Strukturen
erforschen, wie sie in dem untenstehenden
Bild abgebildet sind, so müssen die Teilchen kleiner als die zu untersuchenden
Objekte sein. Das bedeutet, dass sie einen sehr großen Impuls bzw.
eine sehr kleine Wellenlänge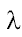
besitzen müssen. Dies erreicht man, indem man ihnen große Energie verleiht.
|
|
|
|
|
|
