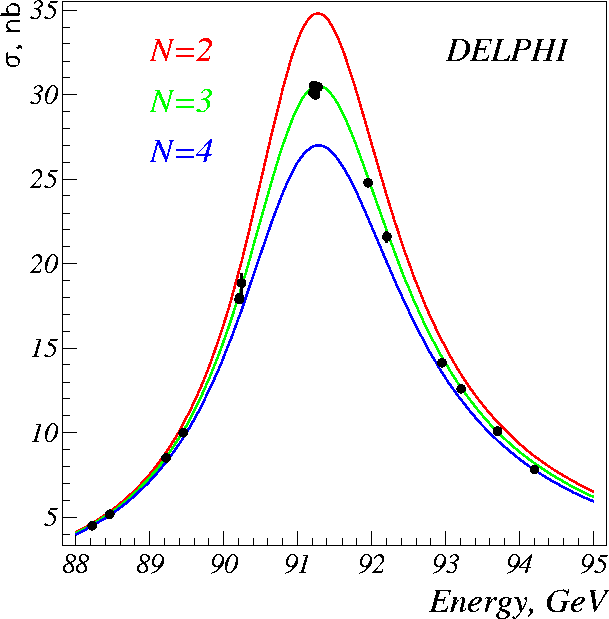
The reason is the particles called neutrinos that escape the detector unseen. These account for about 20% of all Z particle decays, that's why if you add up the branching ratios to visible particles (listed above), you only get 80%.
You can correct your results for invisible decays quickly by dividing the total number of events you looked at by 0.8 and then recalculating your branching ratios with this as the total number of events. So, for example, if you looked at all 100 events, you would get 125. In other words, you are assuming that for those 100 events, 25 Zs were produced and decayed into neutrinos unseen by the detector, and are not in the file.
Do your recalculated results agree with the published ones?

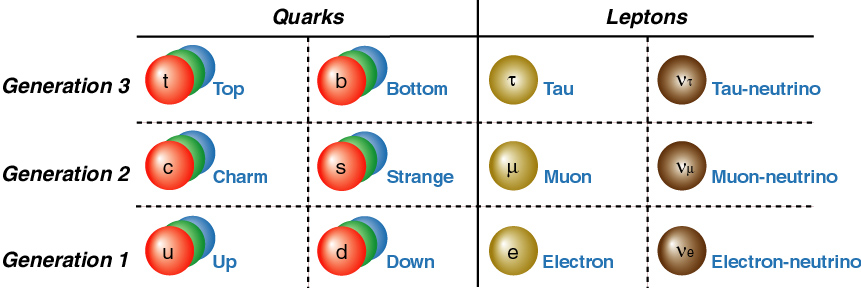
If you have read the pages about matter and interactions, you'll remember that matter particles are grouped into three families. The lightest family consists of particles called up-quarks, down-quarks, electrons and electron-neutrinos. It is the quarks and electrons from this family that make up all of ordinary matter.
The heavier families are made up of particles very similar to but more massive than those of the lightest family. The muons and taus are the heavy cousins of the electrons, and they each have associated neutrinos. Collectively, the electrons, muons, taus and neutrinos are called leptons.
As long as the energy of a collision is high enough to make the heavier leptons, nature shows no preference for one kind of charged lepton over any other. That's what lepton universality means, and it's why the branching ratio is the same for electron-positron pairs, muon-antimuon pairs and tau-antitau pairs.
Now think about the electrically neutral leptons, the neutrinos. Nature also treats all of them equally, so a Z is just as likely to decay into a neutrino-antineutrino pair of the electron, muon, or tau type.
But there is a difference between the neutral and charged leptons. It turns out that a Z is twice as likely to decay into a neutral lepton-antilepton pair as into a charged lepton-antilepton pair. That's why the Z decays we see in the detector account for only about 80% of the total.