Auflösung:
Bei gleichmäßigem "Aufgehen" des Hefekuchenteigs in alle Richtungen sind die Relativgeschwindigkeiten zwischen den Rosinen
proportional
zu ihren Entfernungen voneinander. Je größer die Entfernung zwischen zwei Rosinen, um so schneller entfernen sie sich bei der Ausdehnung voneinander. Deine Messwertepaare sollten im Koordinatenkreuz also auf einer Geraden liegen.
An dieser Eigenschaft erkennt man eine gleichmäßige Ausdehnung des Teiges und kann andere Hypothesen wie "Zerfließen" ausschliessen.
Diese Gerade ist sogar unabhängig davon, welche Rosine Du Dir als Deine "Heimatrosine" ausgesucht hast. Du bekommst dann zwar andere Messpunkte, aber immer auf genau der gleichen Geraden. Weit weg von der Oberfläche ist also kein Punkt im Hefeteig besonders ausgezeichnet.
|
Dies ist hier noch einmal in einem anderen Beispiel dargestellt: 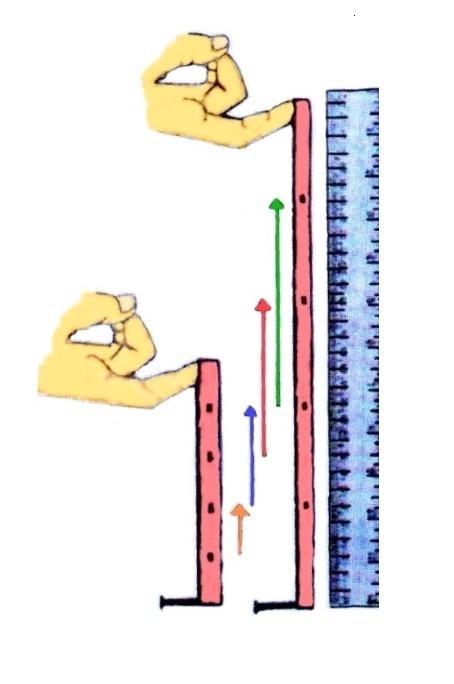
In der Abbildung kannst Du ein Gummiband erkennen, auf dem in gleichen Abständen Punkte gemalt sind. Dehnt man das Band, so ändern sich die Abstände zwischen den Punkten. Die verschiedenfarbigen Pfeile zeigen anhand des Lineals, wie weit sich jeder Punkt von seiner Ausgangslage entfernt hat. Je größer der Abstand eines Punktes zu einem Bezugspunkt, hier der Nagel, umso größer die Zunahme des Abstands nach der Ausdehnung. Je weiter sich ein Punkt in der gleichen Zeit entfernt hat, um so schneller hat er sich natürlich auch relativ zum Bezugspunkt bewegt.
|
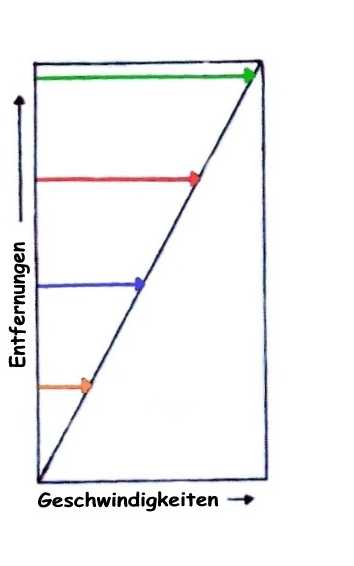
In dem Koordinatenkreuz werden die Abstände (Pfeile) bzw. die Relativgeschwindigkeiten mit einander verglichen, indem die Pfeilspitzen verbunden werden. Anhand der entstandenen Geraden kannst Du sehen, dass die Geschwindigkeiten der Punkte proportional zu ihrer Entfernung vom Fixpunkt, dem untersten Punkt auf dem Gummiband, sind. |
zurück