Momentum
En el uso habitual, el momento se define como el producto de la masa por la velocidad de algún objeto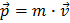 
. Sin embargo, en LHC todas las partículas viajan próximas a la velocidad de la luz ( v=0,999999991c para protones acelerados), antes y después de la colisión. Por ello tienes que utilizar la teoría de la relatividad especial de Einstein y la fórmula para el momento es un poco más complicada, aunque todavía manejable
Comenzamos con la famosa fórmula de Einstein
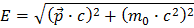
Aquí E indica energía, p momento, m masa y c la velocidad de la luz. El momento es un vector con tres proyecciones sobre los tre ejes (x,y,z), y, si no sabes lo que es un vector, sigue Vectors.
Si haces un poquito de álgebra (simplemente caminando entre los argumentos de la fórmula) puedes expresar la magnitud del momento como función de la energía y la masa
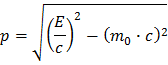
En la naturaleza, el momento se conserva. Est significa lo siguiente: Lo que entra sale, que en colisiones de partículas significa que pantes=pdespués. Para un bosón Z decayendo en un par electrón-positrón significaría pZ = pe- + pe+.
Pregunta de test: En la versión usual del momento p=mv, nos encontramos con un problema en el caso de objetos sin masa como el fotón, pues su momento sería cero. ¿Qué pasa con el momento en el caso de partículas sin masa en la versión de momento de la relatividad especial?