Identify with mass!
Hold on! You are about to dig into some important physics concepts!
In the more complete version of Einstein’s formula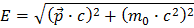 
, E is the energy of the particle, p its the momentum and m0 its the mass of the particle when at rest. It so happens that this definition of mass is conserved in Nature and is called “Invariant Mass”. Shuffling the formula we get:
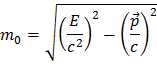
Since this quantity is conserved we can use it to infer the mass of a decaying (“mother”) particle: You measure the energy and momentum of the decay products, from which the mass of the “mother” particle is inferred, since what comes in must go out. Quite straightforward and simple, isn't it?
In the case of a Z boson decaying to an electron (e-) positron (e+) pair the sum of energies and momenta of the electron and positron lead to the mass of the Z boson in the following way:
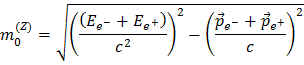
The Z boson energy and momentum, EZ=Ee- + Ee+ and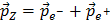 
, are hence known because the ATLAS detector can measure the energy and momentum of the decay-products. That means you have all you need to infer the mass of the Z boson, or that of other particles like J/ψ and Υ!
In fact this, so-called invariant mass method works for a variety of combinations of decay products, such as γγ, l+l- (l=e,μ), l+l-l+l-, and more, as you will find out when studying the Z boson, searching for the Higgs boson, or even exploring the Unknown!