Poszukiwanie cząstek poprzez masę
W tym rozdziale zapoznamy się z narzędziami, które będą potrzebne do dalszej pracy, z wykorzystywanymi w tym celu metodami fizycznymi i obliczeniami matematycznymi. Używając ich ponownie odkryjemy bozon Z i inne znane cząstki, poszukamy bozonu Higgsa, a także spróbujemy poszukać Nieznanego.
Dla upewnienia się, że w zderzeniach powstała jakaś cząstka, nie tylko rozpoznamy produkty jego rozpadu, jak pary mion-antymion, elektron-pozyton lub foton-foton, ale i zrekonstruujemy prawidłową masę rozpadającej się cząstki.
Przekonamy się, że masa jest taką własnością cząstki, która wraz z innymi może być wykorzystana do jednoznacznej identyfikacji cząstki.
Dla zrozumienia jak oblicza się masę cząstki trzeba wiedzieć, co to jest elektronowolt (eV), i znać pojęcia pędu oraz wektora. Odpowiednie objaśnienia można znaleźć w działach Jednostki energii, Pęd or Wektory.
Skorzystamy ze wzoru Einsteina na energię relatywistyczną w pełnej wersji, przekształconego z uwzględnieniem podstawowego prawa Natury: energia i pęd są zachowane we wszystkich procesach fizycznych. Dla układu cząstek te wielkości przed i po zderzeniu lub rozpadzie są takie same.
Na kolejnej stronie wyjaśnimy wzór pozwalający na obliczenie masy rozpadającego się “rodzica”, pod warunkiem, że znane są pewne parametry.
Oto jego postać dla rozpadu bozonu Z na e+e-!
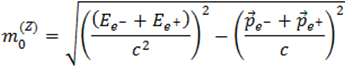
W tym pięknym wzorze m oznacza masę, E - energię, a p - pęd. Prędkość światła jest oznaczana przez c. Indeksy dolne e i Z oznaczają odpowiednio elektron i bozon Z.
A jak będziemy szukali bozonu Higgsa? Ponieważ jego rozpad na elektrony i miony ma w Modelu Standardowym bardzo małe prawdopodobieństwo, lepiej jest badać przypadki z dwoma fotonami lub czterema leptonami.
Tak więc dla H→γγ, użyjemy wzoru podanego powyżej, zamieniając Z na H oraz e na γ. To tyle!
Dla rozpadu H→llll trzeba we wzorze dodać energie i pędy nie dwu cząstek, ale czterech leptonów i nazwać “rodzica” H zamiast Z. Czy to nie jest proste?
W następnym rozdziale dowiemy się więcej!