Vektorer
Måske har du lagt mærke til, at der er en pil over impulsen: 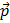 . Husk, at den dagligdags definition af impuls er hastighed gange masse:
. Husk, at den dagligdags definition af impuls er hastighed gange masse: 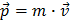 og du kan se, at hastigheden også er mærket med en pil. Det betyder at den er en vektor. Hermed mener man at den har en størrelse og en retning i rummet. Det er meget naturligt, for hvis du har en hastighed af en bestemt størrelse bevæger du dig også i en bestemt retning. Når man laver matematiske operationer med vektorer skal de behandles med særlig omhu. Vi kan opløse vektoren, som peger i en eller anden retning i rummet, efter hvor meget den peger i de retninger, x, y og z vi har valgt som vores koordinatsystem. Produktet af to impulsvektorer bliver en skalar, dvs. et tal uden retning:
og du kan se, at hastigheden også er mærket med en pil. Det betyder at den er en vektor. Hermed mener man at den har en størrelse og en retning i rummet. Det er meget naturligt, for hvis du har en hastighed af en bestemt størrelse bevæger du dig også i en bestemt retning. Når man laver matematiske operationer med vektorer skal de behandles med særlig omhu. Vi kan opløse vektoren, som peger i en eller anden retning i rummet, efter hvor meget den peger i de retninger, x, y og z vi har valgt som vores koordinatsystem. Produktet af to impulsvektorer bliver en skalar, dvs. et tal uden retning:
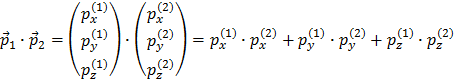
Der er ingen komponenter som blander en retning med en anden, da de bare er 0. Læg også mærke til, at der ikke er nogen pil over leddene i resultatet. Det er fordi (skalar-)produktet af to vektorer bare er et tal (en skalar).