1.
Shrnutí
Náplní tohoto cvičení je
hledání podivných částic produkovaných v protonových
srážkách na urychlovači LHC a zaznamenaných detektorem ALICE.
Základem je hledání V0 rozpadů, jako jsou ![]() ,
, ![]() ,
a kaskádových rozpadů, jakým je například
,
a kaskádových rozpadů, jakým je například ![]() . Jednotlivé události budou
analyzovány vizuálně pomocí ALICE event display
v prostředí ROOT. Identifikace podivných částic je
založena na topologii jejich rozpadu společně s identifikací
částic vzniklých při rozpadu. Pro ověření, že
skutečně jde o hledané částice je využíván
výpočet invariantní hmotnosti z informací o zaznamenaných
dráhách.
. Jednotlivé události budou
analyzovány vizuálně pomocí ALICE event display
v prostředí ROOT. Identifikace podivných částic je
založena na topologii jejich rozpadu společně s identifikací
částic vzniklých při rozpadu. Pro ověření, že
skutečně jde o hledané částice je využíván
výpočet invariantní hmotnosti z informací o zaznamenaných
dráhách.
V následujícím textu bude nejprve
stručně představen experiment ALICE, stejně tak i jeho
fyzikální cíle a motivace pro uskutečnění této analýzy. V
dalším bodě bude vysvětlena metoda sloužící pro
identifikaci podivných částic a použitý softvér pro analýzu. Následně bude
podrobně popsán postup při cvičení a prezentaci
výsledků. Na závěr bude objasněn postup při
shromažďování a
sčítávání výsledků.
2.
Úvod
ALICE (A Large
Ion Collider Experiment), sloužící ke studiu
srážek těžkých iontů, je jedním ze
čtveřice velkých experimentů umístěných na Large Hadron Collideru v CERNu. Stejně tak zkoumá i proton-protonové srážky.
Ty slouží primárně pro srovnání s výsledky
jádro-jaderných srážek, mimoto poskytují data pro studium fyziky
proton-protonových srážek jako takových. Detektor ALICE byl
navržen tak, aby byl schopný se vypořádat s vysokými
počty částic, jaké jsou předpokládany
ve srážkách jader olova při extrémních energiích LHC.
3.
Fyzika na ALICE
Kvarky jsou vázány v protonech a
neutronech silou známou jako silná interakce. Ta je zprostředkována
výměnou částic, které nazýváme gluony. Silná interakce
také způsobuje, že protony a neutrony jsou vázány v jádrech
atomů.
Přestože je v
dnešní době silná interakce již z velké části pochopená, na
dvě základní otázky stále neznáme odpověď: proč jsou kvarky
uvězněny a co způsobuje hmotnost. Dle našich předpokladů
odpovědi leží ve změnách vlastností vakua
způsobených silnou interakcí.
Ačkoliv je známo, že
kvarky jsou elementární částice, ze kterých jsou složeny
veškeré známé hadrony, žádný izolovaný kvark nikdy
nebyl pozorován. Kvarky, stejně tak i gluony, jsou podle všeho permanentně
uzavřeny ve složených částicích, jakými jsou
například proton nebo neutron. Tato vlastnost je známá jako
uvěznění. Doposud však nebylo odhaleno, co ji způsobuje.
Současná teorie
vysvětlující silnou interakci (Kvantová Chromodynamika) předpovídá, že
při velmi vysokých teplotách a velmi vysokých hustotách
nebudou kvarky ani gluony vázány uvnitř částic. Naopak budou
volně koexistovat ve stavu, který nazýváme kvark-gluonové
plazma.
K přechodu do této fáze by
mělo dojít v případě, kdy teplota přesáhne jistou kritickou
hodnotu. Ta by se měla pohybovat okolo 200 miliard
stupňů...což je asi 100000-krát více, než teplota
slunečního jádra! Takto vysoké teploty panovaly ve Vesmíru pouze po
několik málo miliontin sekundy po Velkém Třesku. Domníváme se,
že tehdy byl Vesmír skutečně ve stavu kvark-gluonového plazmatu.
Reprodukovat takto extrémní
podmínky a tím uvolnit kvarky a gluony lze srážením
těžkých jader urychlených na rychlost blízkou rychlosti
světla. Uvolněné kvarky a gluony se pak dále srážejí mezi sebou,
vytvářeje tak prostředí v tepelné rovnováze, kterým je
kvark-gluonové plazma. To se dále rozpíná a chladne až na teplotu
(přibližně 1012 stupňů), při které se
kvarky a gluony opět začnou shlukovat a formovat obvyklou hmotu. K
návratu do běžného stavu dochází pouhých 10-23
sekund od začátku srážky. ALICE bude tedy studovat vznik a vlastnosti
tohoto nového stavu hmoty.
4.
Nárůst podivnosti jako znak kvark-gluonového plazma
Stanovit a studovat vlastnosti
kvark-gluonového plazma můžeme skrze takové kvarky, které se
normálně v přírodě nevyskytují. Jedna z metod
používaných v experimentech vychází z myšlenky nárůstu
podivnosti. Jde o první pozorovanou veličinu kvark-gluonového plazmatu,
navrženou v roce 1980. Na rozdíl od kvarků up a down
nejsou podivné kvarky do reakce přineseny sráženými jádry.
Jakýkoliv pozorovaný podivný kvark nebo antikvark musí
tedy vzniknout z kinetických energií jader. Hmotnost podivných
kvarků, resp. antikvarků, odpovídá energii, při které dochází k
rozpadu protonu, neutronu a dalších hadronů na jednotlivé kvarky.
Množství podivných kvarků je tudíž značně
citlivé na podmínky, struktuře a dynamice hmoty ve volném stavu. V
případě jejich vysokého počtu můžeme usuzovat, že
volnosti bylo dosaženo.
V praxi můžeme
nárůst podivnosti zaznamenat při počítání počtu
podivných částic (částice obsahující alespoň jeden
podivný kvark) a následným výpočtem poměru
podivných částic k částicím, jež žádný podivný
kvark neobsahují. Převyšuje-li tento poměr hodnotu
předpovězenou teoretickými modely, které tvorbu
kvark-gluonového plazmatu nepředpokládají, zjišťujeme nárůst
podivnosti.
Alternativně,
pro srážky olova, je počet podivných částic normalizován počtem
nukleonů, které se zúčastnily srážky a porovnán se
stejným poměrem v protonových srážkách.
5.
Podivné částice
Jak už bylo zmíněno,
podivné částice obsahují alespoň jeden podivný kvark. Tato
vlastnost může být vyjádřena pomocí kvantového čísla
"podivnosti". Nejlehčím neutrálním podivným mezonem,
respektive baryonem, je kaon ![]() , respektive hyperon Λ (uds).
, respektive hyperon Λ (uds).
Budeme studovat jejich rozpady ![]() -,
-, ![]() .
Během těchto rozpadů dochází ke změně podivnosti,
neboť částice v nich vzniklé sestávají pouze z kvarků up a down. Tudíž nejde o silné procesy (ty by
navíc trvaly velmi krátce, s τ = 10-23 s), nýbrž o
slabé procesy, při kterých podivnost zachována být může
(ΔS=0), nebo nemusí; v takovém případě ΔS=1. Střední
doba života částic podléhajících slabému rozpadu se pohybuje mezi 10-10
a 10-8 s. Pohybují-li se tyto částice rychlostí blízkou
rychlosti světla, urazí před rozpadem průměrně
několik centimetrů od místa svého vzniku.
.
Během těchto rozpadů dochází ke změně podivnosti,
neboť částice v nich vzniklé sestávají pouze z kvarků up a down. Tudíž nejde o silné procesy (ty by
navíc trvaly velmi krátce, s τ = 10-23 s), nýbrž o
slabé procesy, při kterých podivnost zachována být může
(ΔS=0), nebo nemusí; v takovém případě ΔS=1. Střední
doba života částic podléhajících slabému rozpadu se pohybuje mezi 10-10
a 10-8 s. Pohybují-li se tyto částice rychlostí blízkou
rychlosti světla, urazí před rozpadem průměrně
několik centimetrů od místa svého vzniku.
6.
Hledání podivných částic
Cílem tohoto cvičení je
hledání podivných částic vzniklých z
proton-protonových srážek na LHC zaznamenaných na
experimentu ALICE.
V předešlé sekci
již bylo zmíněno, že podivné částice nežijí dlouho,
ale rozpadají se krátce po svém vzniku. Přesto žijí
dostatečně dlouho na to, aby urazily vzdálenost několika
centimetrů od bodu vzniku. Budeme tedy hledat částice vzniklé jejich
rozpadem, nutně pocházející ze stejného sekundárního vrcholu.
Neutrální podivné částice,
jakými jsou např. kaony a lambdy, vytvářejí při rozpadu
charakteristické obrazce, nazývané V0. Několik centimetrů od
místa vzniku mateřské částice zanikají, místo nich se objeví dvě
opačně nabité částice. Působením magnetického pole ALICE
solenoidu jsou jejich dráhy zakřiveny v opačných směrech.
Kladně nabité částice jsou na následujících obrázcích vyznačeny
červeně; záporně nabité jsou vykresleny modře.
Budeme hledat rozpady:
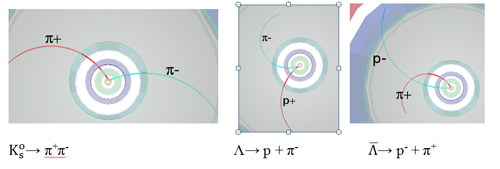
Všimněte si, že
první rozpad je kvazisymetrický, zatímco v
případě produkce pionu a protonu je dráha protonu více
zakřivená. Vzhledem ke své vyšší hmotnosti nese proton
většinu původní hybnosti.
Mimoto budeme hledat nabité
podivné částice, rozpadající se kaskádově, jako příklad
uveďme ![]() .Tato se rozpadá na Λ a Ļ-,
lambda se dále rozpadá na proton a Ļ-. Pion vzniklý prvním
rozpadem budeme nazývat "samotář", jeho dráha je
vyznačena fialově.
.Tato se rozpadá na Λ a Ļ-,
lambda se dále rozpadá na proton a Ļ-. Pion vzniklý prvním
rozpadem budeme nazývat "samotář", jeho dráha je
vyznačena fialově.
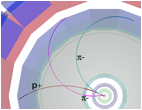
Ξ-→Ļ-Λ→ Ļ-
p + Ļ-
Hledání V0 rozpadů vychází
z topologie společně s rozpoznáním jeho produktů.
K potvrzení správnosti určení částice slouží
výpočet její hmotnosti. Tu zjistíme z hmotnosti a hybnosti
dceřiných částic, jak je popsáno v další části.
7.
Výpočet invariantní hmotnosti
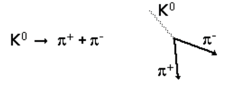
Mějme rozpad neutrálního
kaonu na dva nabité piony (viz. obrázek).
Nechť E, p a m jsou celková energie, hybnost
(vektor!) a hmotnost mateřské částice (![]() .).
.).
Nechť E1, p1 a m1 jsou celková
energie, hybnost a hmotnost dceřiné částice s číslem 1 (Ļ+) a E2, p2 a m2 jsou celková
energie, hybnost a hmotnost dceřiné částice s číslem 2 (Ļ-).
Zákon zachování energie
E = E1+E2 (1)
Zákon zachování hybnosti p = p1+p2 (2)
Z relativity (předpokládáme c=1) E2
= p2 + m2 (3)
kde p=|p|
je velikost vektoru hybnosti p.
To samé samozřejmě platí pro dceřiné
částice
E12 = p12
+ m12 (4)
E22 = p22
+ m22
(5)
kde p1=|p1| a p2=|p2| jsou velikosti p1
a p2.
Z uvedených vzorců
vyjádříme
m2 = E2 - p2 =
(E1+E2)2 - (p1+p2)2 = E12
+ E22 +2E1E2 - p1 .p1
- p2.p2 - 2 p1.p2 (6)
kde jsme zavedli skalární součin p1.p2 vektorů p1 and p2, který je roven součtu součinů
jejich složek x, y a z:
p1 .p2 = p1x
p2x + p1y p2y + p1z p2z (7)
p1 .p1 = p1x 2 + p1y
2 + p1z
2 = p12 (8)
p2 .p2 = p2x 2 + p2y
2 + p2z
2 = p22 (9)
Rovnici
(6) převedeme na tvar:
m2 = E12 + E22
+2E1E2 - p12
- p22
-2 p1 .p2
= m12 + m22 +2E1E2
- 2 p1 .p2
(10
)
Hmotnost původní
částice můžeme tudíž vypočíst z hmotnosti a
složek hybnosti vzniklých částic. Hmotnosti m1 a m2
jsou známe, neboť dceřiné částice jsou identifikovány pomocí
vícero detektorů na ALICE.
Hybnosti p1 a p2
lze zjistit změřením poloměru křivosti trajektorie
příslušných částic v závislosti na známém magnetickém
poli.
Ve cvičení využijeme
tři složky hybnosti z každé dráhy ztotožněné s V0
rozpadem.
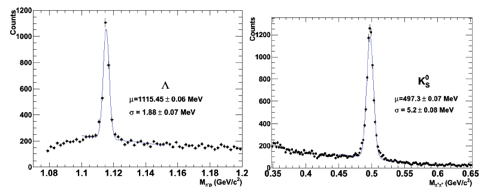
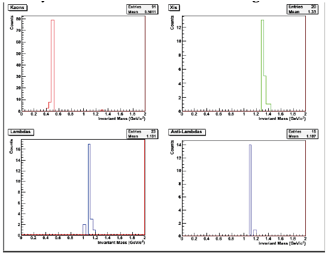
Z výpočtu invariantní
hmotnosti získáme distribuce podobné těm, které jsou vyobrazeny níže.
Distribuce vlevo představuje rozložení hmotností v případě
pion-protonových párů. Maximum odpovídá hmotnosti lambda, spojené
pozadí vzniklo náhodnými kombinacemi pionů a protonů. Ty byly
buď špatně identifikovány, nebo nepocházely ze stejného
sekundárního vrcholu. Napravo najdete hmotnosti spočtené z párů nabitých
pionů, maximum odpovídá ![]() .
.
8.
Program a jeho použití

Cvičení
bude probíhat v programu ROOT za pomocí ALICE event
display, vizuálního zobrazovače událostí. Na vašem počítači
bude již dopředu spuštěný terminál (to abyste byli
ve správném adresáři). Do něj napište root masterclass.C'. Objeví se okénko (které
můžete vidět na obrázku) nabízející na výběr Demo
(demonstrační režim), Student (studentský režim) a Teacher (učitelský režim).
Studentský režim použijete pro analýzu a vizuální
hledání V0 rozpadů, učitelský režim umožňuje
sběr a sčítání vyhodnocených dat.
Možnost Demo spustí ukázku
rozpadů ![]() , Λ,
, Λ, ![]() a
a ![]() . Zvolíte-li Student, zobrazí se
Vám okno z dalšího obrázku.
. Zvolíte-li Student, zobrazí se
Vám okno z dalšího obrázku.
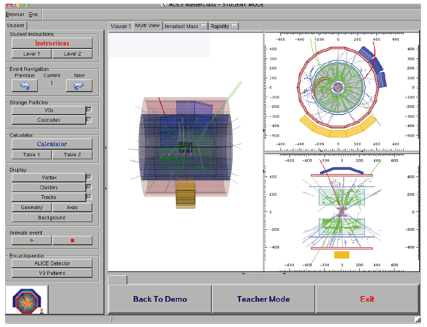
Ve sloupci nalevo najdete
následující možnosti: Instructions (instrukce), Event Navigation
(výběr událostí), tlačítka vyhledávající V0 a Cascade
(kaskádový rozpad), Calculator, tlačítka
umožňující zobrazení různých informací o události
(např. dráhy částic, změna geometrie detektoru). Dále zde
naleznete Event Animation
(vizualizace události) a Encyklopedii obsahující stručný popis
detektoru ALICE a jeho hlavních součástí, stejně tak jako obrazce z
V0 rozpadů a příklady
olověných srážek.
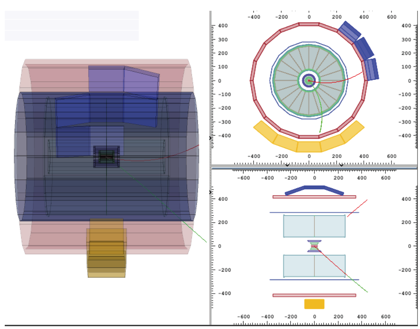
Každá událost je zobrazena
ze tří pohledů: 3D view, rφ projection
(příčný řez) a rz projection (podélný řez). Jde o
zjednodušenou verzi vizualizace událostí používaných na ALICE.
Můžete si vybrat, jaké informace chcete pro danou událost zobrazit.
Kliknutím na příslušné tlačítko zobrazíte všechny shluky (Clusters) a dráhy (Tracks)
zaznamenané v události. Výběrem možnosti V0 a Cascades se zviditelní všechny příslušné
rozpady, byly-li zaznamenány. Naleznete-li nějaký rozpad,
můžete zbytek informací, které Vás v daný moment nezajímají,
schovat. Ve V0 jsou kladně nabité dráhy znázorněny červeně,
záporně modře. Pion "samotář" z kaskádového rozpadu
bude zobrazen fialově.
Kliknutím na jednotlivé dráhy
zobrazíte hodnoty složek hybnosti a hmotnost částice v malém okénku
(další obrázek, vpravo). Ty mohou být zkopírovány do kalkulátoru,
který z nich vypočte invariantní hmotnost původní částice
(jakým způsobem je popsáno v předešlé části).
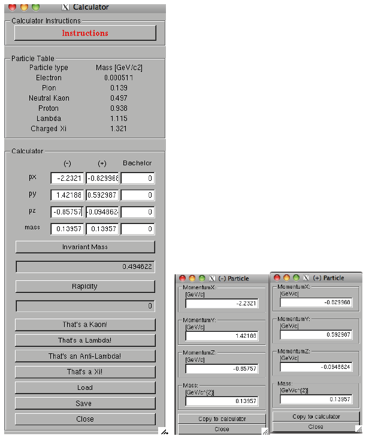
Program obsahuje i
čtveřici histogramů reprezentujících invariantní hmotnosti
hledaných částic. Důkladným prozkoumáním každého
rozpadu můžete určit mateřskou částici jak z částic
dceřiných, tak z hodnoty hmotnosti (tabulka obsahující hmotnosti
částic je uvedena v kalkulátoru, viz. obrázek). Poté už stačí
jen kliknout na příslušné tlačítko (pro kaon "That's a Kaon" atd.) Tím přiřadíte danou
hodnotu k odpovídajícímu histogramu. Histogramy zobrazíte, kliknete-li na
kolonku Invariant mass, která se nalézá nad
zobrazením události. Pro načtení hodnot do histogramu na něj klikněte
myší.
Program sice poskytuje i
možnost výpočtu rapidity, tato úloha
však přesahuje rámec cvičení.
9.
Cvičení - analýza událostí a hledání podivných částic
Vaším
úkolem bude identifikovat a spočítat počet podivných
částic ve vám přiděleném vzorku událostí, obvyklý
počet událostí ve vzorku je 30. Spusťte tedy studentský
režim a vyberte si vzorek, který budete analyzovat. K dispozici
máte 6 vzorků obsahujících data z proton-protonových srážek o
těžišťové energii 7 TeV. Po
otevření události klikněte na Cluster a Track. Jen tak budete moci
obdivovat složitost zobrazené události stejně jako vysoký
počet vzniklých částic. Většina částic jsou
piony.
Volbou
V0 a Cascades zvýrazníte příslušné
dráhy (vyskytují-li se v zobrazené události). Z topologie V0 se dá
odhadnout typ mateřské částice. Kliknutím na jednotlivé dráhy se
zobrazí náboj, složky hybnosti a invariantní hmotnost příslušné
částice a její nejpravděpodobnější typ. Tyto informace byly
získány z různých detektorů užitých pro
identifikaci částic. Ze vzniklých částic lze již
dopředu odhadnout, o jaký rozpad se jedná. Výpočet
invariantní hmotnosti (sekce 7) slouží k potvrzení Vašeho odhadu.
Porovnejte výsledek s výpočtem na kalkulačce.
Zjistíte-li
hmotnost 497 MeV Ī 13 MeV
(tedy interval hmotností (484; 510) MeV), jedná se o ![]() .
.
Je-li
hmotnost 1115 Ī 5 MeV (interval (1110; 1120) MeV) a vzniknul-li proton a záporně nabitý
pion, našli jste hyperon Λ. Jsou-li dceřinými produkty
antiproton a kladně nabitý pion, jde o rozpad ![]() .
.
Dává-li
výpočet hmotnosti ze tří částic při kaskádovém
rozpadu hodnotu 1321 Ī 10 MeV (interval (1311; 1331) MeV), našli jste ![]() .
.
Podle výsledku vyberte
příslušné tlačítko (It's a Kaon atd.).
Zjištěnou hmotnost tak zaznamenáte do odpovídajícího histogramu.
Může se stát, že
zjištěná hmotnost nebude odpovídat ani jednomu z uvedených
případů. Jde o "pozadí", kdy částice zdánlivě
pocházejí ze stejného sekundárního vertexu, ten byl však nesprávně
identifikován. Takovéto rozpady ignorujte.
10. Prezentace výsledků
V této
tabulce jsou shrnuty všechny výsledky. Sloupec „Real data“ obsahuje
počty ![]() , Λ, anti-Λ a Ξ-, které jste našli (za předpokladu, že jste správně
klikali na „This is a Kaon,Lambda …“ tlačítko).
, Λ, anti-Λ a Ξ-, které jste našli (za předpokladu, že jste správně
klikali na „This is a Kaon,Lambda …“ tlačítko).
Také je možné se
podívat na histogramy invariantních hmotností a zkontrolovat počty pro
každý typ částice. Když jste zpracovali všechny
události ve vašem souboru, uložte výsledky podle instrukcí v
programu na zpracování.
11.
Ukládání výsledků
Pro ukládání výsledků
přejděte v do učitelského režimu (kolonka Teacher v MasterClass menu). Dále
v Teacher Controls zvolte možnost Get Files, která Vám umožní
získat data z analyzovaných vzorků (každý vzorek musíte
vybrat zvlášť). Nezapomeňte předtím všechny
výsledky nahrát do "učitelského" počítače.
Volbou "Results" (výsledky)
zobrazíte tabulky 1 a 2 s plnou statistikou.
12. Zpracování velkého množství událostí
Grafické
zobrazování srážek na obrazovce je vynikající pomůcka pro kontrolu
kvality dat a jejich rekonstrukce. Pomáhá nám získat představu jak
události vypadají. Avšak
v běžném vědeckém životu se experimentální údaje
nezpracovávají vizuálně – to by bylo časově
příliš náročné. Pro zpracování milionů údajů, které se
den co den na LHC zaznamenávají, je
nutno použít počítačové programy což je účelem této části, kde
budeme hledat V0 ve velkém množství událostí.
V
okně terminálu
změňte adresář (použitím příkazu: cd MasterClass_extended)
a napište root MasterClassesExtended.C. V položce “put
your name here“ mezera, zadejte znaky, které budou sloužit k vytvoření
názvu souboru s výsledky. Vyberte si soubor pro zpracování (v
současné době je k dispozici šest souborů s údaji ze srážek
pp 7TeV obsahující po 2000 událostí);
pak vyberte položku „student“ a začnete zpracování.
Pomocí
položky „Analysis tools“
je možné zpracovat 100 nebo 2000 událostí a vypočítat invariantní
hmotu párů částic, jako ![]() .
Je možné vidět, že spektrum invariantní hmoty je kontinuum
– to je proto, že kombinace vytvořených párů jsou
náhodné, nepocházejí ze společného sekundárního vrcholu srážky a mohou mít
libovolnou hmotnost. Toto je pozadí.
.
Je možné vidět, že spektrum invariantní hmoty je kontinuum
– to je proto, že kombinace vytvořených párů jsou
náhodné, nepocházejí ze společného sekundárního vrcholu srážky a mohou mít
libovolnou hmotnost. Toto je pozadí.
Když
přejdeme k výběru V0, pouze páry drah vycházející ze
společného sekundárního
vrcholu jsou dále uvažovány; vypočte se jejich invariantní hmotnost
na základě informací z drah a hmotností určených
dceřiných produktů.
Můžete vybrat ![]() nebo Λ ( včetně
nebo Λ ( včetně ![]() ). Pokaždé když je ukončené zpracování
souboru událostí (sledujte terminál za hlavním menu), klikněte na obrázek
s invariantní hmotou, aby se vám zobrazily příslušné histogramy.
). Pokaždé když je ukončené zpracování
souboru událostí (sledujte terminál za hlavním menu), klikněte na obrázek
s invariantní hmotou, aby se vám zobrazily příslušné histogramy.
Abychom
mohli najít počet částic daného typu, například ![]() ,
je nutné určit počet událostí v příslušném vrcholu po
odečtení pozadí. Při
prokládání pozadí křivkou (kvadratická funkce), je nutné nejdřív
zvolit rozsah za pomocí posouvače a kliknete na „Fit background“
(Prolož pozadí). Když klikněte na obrazovku, prokládající funkce
je nakreslena do histogramu a
můžete pohledem zkontrolovat, jestli je proložení
v pořádku. Když
nakonec prokládáte signál Gaussovou funkcí nejdříve vyberte část
vrcholu pro proložení. Pro odečtení pozadí jsou použity získané
koeficienty kvadratické funkce; kliknutím
na histogram získáte celkové množství událostí ve vrcholu, počet
událostí z pozadí a ze signálu,
jako také střední hodnotu
Gaussovské funkce ( hmotnost částice) a její šířku.
,
je nutné určit počet událostí v příslušném vrcholu po
odečtení pozadí. Při
prokládání pozadí křivkou (kvadratická funkce), je nutné nejdřív
zvolit rozsah za pomocí posouvače a kliknete na „Fit background“
(Prolož pozadí). Když klikněte na obrazovku, prokládající funkce
je nakreslena do histogramu a
můžete pohledem zkontrolovat, jestli je proložení
v pořádku. Když
nakonec prokládáte signál Gaussovou funkcí nejdříve vyberte část
vrcholu pro proložení. Pro odečtení pozadí jsou použity získané
koeficienty kvadratické funkce; kliknutím
na histogram získáte celkové množství událostí ve vrcholu, počet
událostí z pozadí a ze signálu,
jako také střední hodnotu
Gaussovské funkce ( hmotnost částice) a její šířku.
Pro
uložení histogramů si nejprve vyberte adresář kam je chcete
uložit ( automaticky nastaveno na „Teacher“) a
pak vyberte podadresář: K0s
(pro Kaony), Lambda (společně pro Λ a ![]() ). Kliknutím na 1,2,3 a 4 uložíte histogramy
zobrazené nahoře vlevo, nahoře vpravo, dolu vlevo a dolu vpravo.
). Kliknutím na 1,2,3 a 4 uložíte histogramy
zobrazené nahoře vlevo, nahoře vpravo, dolu vlevo a dolu vpravo.
Může
být složité proložit data z 2000 událostí – bude to
lehčí s větším množstvím, poté co jste sečetli
všechny výsledky, jak bude popsáno v další sekci.
13. Sčítání všech
výsledků ze zpracování velkého množství událostí
Zvolte
„Teacher mode“ v menu „large-scale
analysis“ (zpracování velkého množství). Pak
volba
„Get Files“ (Vzít soubory) pracuje následovně: Kliknutím na „Teacher“, automaticky nastavěný adresář,
můžete zvolit podadresáře
pro Kaony (K0s), Λ a ![]() (Lambda). Když jste již vybrali
adresář („Teacher“ může být
nahrazen adresářem podle vaší volby, kam jste uložili své
histogramy) a podadresář, kliknete na
1, 2, 3 a 4 – všechny soubory s v tomto
podadresáři budou sečteny (informace o počtu a velikosti
histogramů se zobrazí na terminálu za menu); když klikněte na
obrazovku, zobrazí se vám výsledný histogram na horní levé (1), horní pravé (2), dolní levé (3) a dolní pravé (4)
části obrazovky.
(Lambda). Když jste již vybrali
adresář („Teacher“ může být
nahrazen adresářem podle vaší volby, kam jste uložili své
histogramy) a podadresář, kliknete na
1, 2, 3 a 4 – všechny soubory s v tomto
podadresáři budou sečteny (informace o počtu a velikosti
histogramů se zobrazí na terminálu za menu); když klikněte na
obrazovku, zobrazí se vám výsledný histogram na horní levé (1), horní pravé (2), dolní levé (3) a dolní pravé (4)
části obrazovky.
Pro
získání informace o celkovém počtu částic daného typu následujte
postup prokládání pozadí a signálu tak jak je popsán v předešlé
sekci.
14. Výpočet
výtěžků částic
Za
pomocí informace která vám bude poskytnuta potom co ukončíte zpracování (například účinnost
rekonstrukce drah pro různé typy částic) vypočtete
výtěžek (počet částic vzniklých při
jedné srážce) pro každý typ V0.
15. Postup řešení
Vizuální
část
1. Prohlédněte, si příklady V0
rozpadů a seznamte se s nástroji (V0 vyhledávač,
kalkulačka, histogramy).
2. Vizuálně zpracujte soubor
s 30 V0 události.
3. Sečtete výsledky ze
všech skupin.
Zpracování
velkého množství událostí
4.
Zpracujte 2000 událostí. Zkoumejte
rozdělení hmotnosti kombinatorického pozadí.
5.
Zpracujte 2000 událostí: hledejte ![]() /
proložte pozadí / proložte vrchol.
/
proložte pozadí / proložte vrchol.
6.
Zpracujte 2000 událostí: hledejte Λ a
![]() /
proložte pozadí / proložte vrchol.
/
proložte pozadí / proložte vrchol.
7.
Sečtete výsledky ze všech skupin.